Universal arithmetick: or, a treatise of arithmetical composition and resolution. Written in Latin. Translated by the late Mr. Ralphson; and revised and corrected by Mr. Cunn. To which is added, a treatise upon the measures of ratios, by James Maguire, A.M. The whole illustrated and explained, in a series of notes, by the Rev. Theaker Wilder, D.D.
London: for W. Johnston, 1769.
3rd Edition. Hardcover. Very Good. Item #003181
Two parts in one volume. 8vo (203 x 124 mm). viii, 1-346, [5], 348-464, [1], 468-536; [2], 63, [3] pp. 3 pages errata and 8 folding engraved plates bound at end of part II. Contemporary mottled calf, spine with 5 raised bands and gilt-lettered red morocco label (joints cracked towards head of spine, extremities rubbed, corners little scuffed). Text and plates very little browned only, a few pages with faint foxing. Provenance: William Morrison (incribed on front pastedown and title), A. Mc.Donald (inscribed on first flyleaf and dated 1890). A very good, unstained copy in untouched contemporary binding. Collated complete. ----
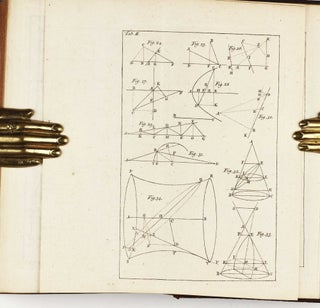
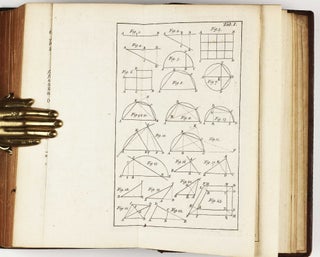
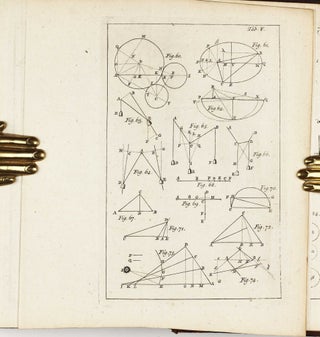
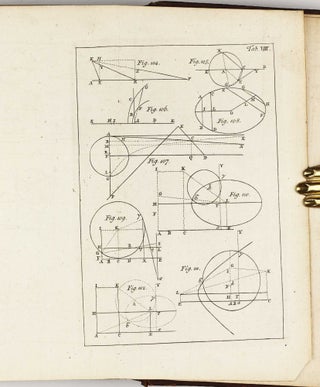
Babson 203; Gray 285. Third and last edition in English, and the only one edited by Theaker Wilder for the use of his students at Dublin. Very rare on the market with no copy sold at auction since 1977. Originally published and edited by William Whiston, who succeeded Newton as Lucasian Professor of Mathematics at Cambridge in 1701, "The Universal Arithmetic, which is on algebra, theory of equations, and miscellaneous problems, contains the substance of Newton's lectures during the years 1673 to 1683. Whiston extracted a somewhat reluctant permission from Newton to print it, and it was first published in Latin in 1707. Amongst several new theorems on various points in algebra and the theory of equations Newton here enunciates the following important results. He explains that the equation whose roots are the solution of a given problem will have as many roots as there are different possible cases; and he considers how it happens that the equation to which a problem leads may contain roots which do not satisfy the original question. He extends Descartes's rule of signs to give limits to the number of imaginary roots. He uses the principle of continuity to explain how two real and unequal roots may become imaginary in passing through equality, and illustrates this by geometrical considerations; thence he shews that imaginary roots must occur in pairs. The most interesting theorem contained in the work is his attempt to find a rule (analogous to that of Descartes for real roots) by which the number of imaginary roots of an equation can be determined" (W.W.R. Ball, A Short Account of the History of Mathematics). - Visit our website for additional images!
Price: 4,000 € * convert currency
Delivery time up to 10 days. For calculation of the latest delivery date, follow the link: Delivery times
Lieferzeit max. 10 Tage. Zur Berechnung des spätesten Liefertermins siehe hier: Lieferzeiten