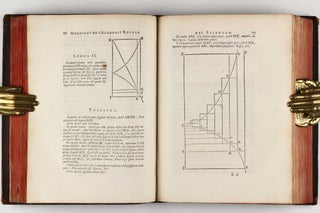
Leibniz' invention of binary arithmetrics

LEIBNIZ, Gottfried Wilhelm.

Nouvelle arithmetique binaire. - Explication de l'arithmétique binaire, qui se sert des seuls caracteres 0 & 1; avec des remarques sur son utilité, & sur ce qu'elle donne le sens des anciennes figures Chinoises des Fohy.

Paris: Jean Boudot, 1705.

1st Edition. Hardcover. Very Good. Item #003257

In: Histoire de l'Academie des Sciences, avec les Mémoires, Année MDCCIII, pp. 58-63 (Histoire), pp. 85-89 (Memoires). Two parts in one volume. Paris: Boudot, 1705. 4to (241 x 182 mm). Title page with large woodcut vignette, woodcut head- and tailpieces, engraved historiated frontispiece, the Mémoires with separate pagination, errata leaf bound at end, 12 (10 folding) engraved plates and a few woodcut text illustrations and diagrams. Entire volume: [10], 148, 467 [1], [2] pp. Bound in 18th century French calf, spine with 5 raised bands gilt-decorated in compartments and with two gilt-lettered morocco labels (boards and extremities rubbed, corners worn). Text only very little browned, occasional minor spotting, faint dampstaining to upper blank margin of several pages, but generally crisp and clean internally. Provenance: Kaiserl. Universitäts-Sternwarte Strassburg (ink stamps to first flyleaf and title leaf recto and verso). ----

FIRST EDITION, FIRST ISSUE of Leibniz' invention of binary arithmetrics. Before Leibniz, Thomas Hariot and Blaise Pascal had already demonstrated number systems other than the decimal and Caramuel y Lobkowitz, in his Mathesis biceps 1670, was the first to publish explicitly on binary arithmetics. However, "Caramuel's contemporaries took so little notice of his work that Leibniz was hailed as the discoverer of the binary system upon publication of his Explication 33 years later in 1703. Many investigators still cite this paper as the first published work on the topic. This technical error is justified in substance, for the test of true publication is the existence of reaction and follow-up, a test failed by Caramuel's work." (Glaser, p.20). The Explication de l'arithmétique binaire by Leibniz appeared in the 1703 volume of the Memoires de l'Academie Royale des Sciences on pages 85-89. This explanation of binary arithmetic was the first publication on this topic to result in a significant impact on the scientific community. Leibniz, now 57, had been a frequent contributor to the Memoires of this Parisian academy. The Berlin academy was not to begin its publications until 1710." (Ibid., p.39).
"Of binary numeration, he writes 'it permits new discoveries (in)... arithmetic ... in geometry, because when the numbers are reduced to the simplest principles, like 0 and 1, a wonderful order appears everywhere.' Concerning the binary calculations themselves '... these operations are so easy that we shall never have to guess or apply trial and error, as we must do in ordinary division. Nor do we need to learn anything by rote.' Certainly Leibniz was not the first to experiment with binary numbers or the general concept of a number base. However, with base 2 numeration, Leibniz witnessed the confluence of several intellectual ideas of his world view, not just the characteristica generalis, but also theological and mystical ideas of order, harmony and creation. Additionally his 1703 paper contains a striking application of binary numeration to the ancient Chinese text of divination, the Yijing (l-Ching or Book of Changes). Early in life Leibniz developed an interest in China, corresponded with Catholic missionaries there, and wrote on questions of theology concerning the Chinese. Surprisingly he believed that he had found an historical precedent for his binary arithmetic in the ancient Chinese lineations or 64 hexagrams of the Yijing. This, he thought, might be the origin of a universal symbolic language. A hexagram consists of six lines atop one another, each of which is cither solid or broken, forming a total of 64 possibilities, while a grouping of only three such lines is called a trigram (or cova). Leibniz lists the eight possible trigrams in his exposition on binary arithmetic, juxtaposed with their binary equivalents. He had been in possession of his ideas concerning binary arithmetic well before his 1703 publication. In 1679 Leibniz outlined plans for a binary digital calculating machine, and in 1697 he sent a congratulatory birthday letter to his patron Duke Rudolph August of Brunswick, in which he discusses binary numeration and the related creation theme with 0 denoting nothing and I denoting God. Furthermore, Leibniz sent the French Jesuit Joachim Bouvet (1656-1730) an account of his binary system while Bouvet was working in China. The Jesuits are an educational order of Catholic priests, who, while in China, sought the conversion of the Chinese to Christianity, hopefully by the identification of an ancient theology common to both religions. Bouvet began a study of the Yijing, viewing this text as the possible missing link between the two religions. It was from this Jesuit priest that Leibniz received the hexagrams attributed to Fuxi, the mythical first Emperor of China and legendary inventor of Chinese writing. In actuality, the hexagrams are derived from the philosopher Shao Yong's (1011-1077) Huangji jingshi shu (Book of Sublime Principle Which Governs All Things Within the World). Shortly after receiving Bouvet's letter containing the hexagrams and Bouvet's identification of a relation between them and binary numeration." (Hopkins, p.170).
References: Glaser, A., History of Binary and Other Non-Decimal Numeration, Anton Glaser, Southhampton, PA, 1971; B. Hopkins, Resources for Teaching Discrete Mathematics, 2009, p.170). - Visit our website to see more images!

Price: 13,500 €  *  convert currency